Ideal: My Quest For The KuNDali Solid

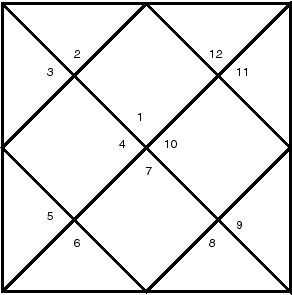
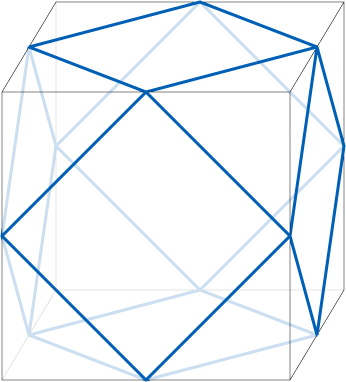
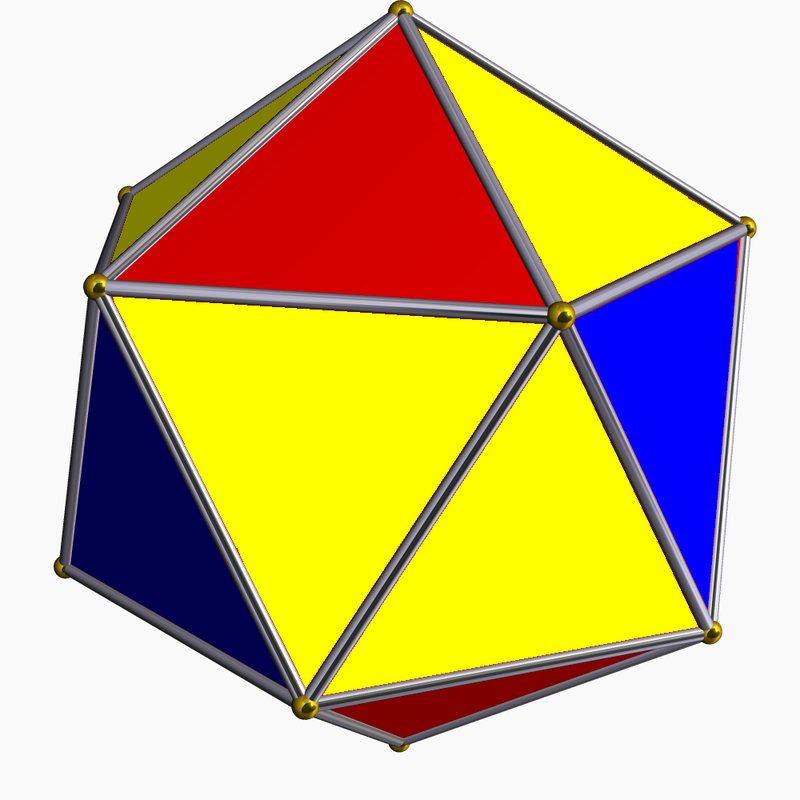
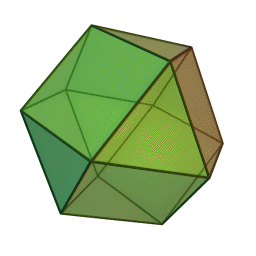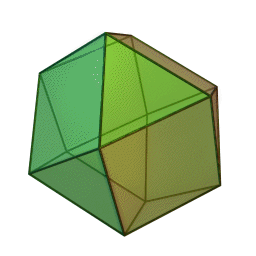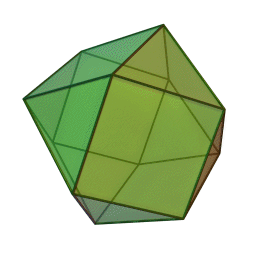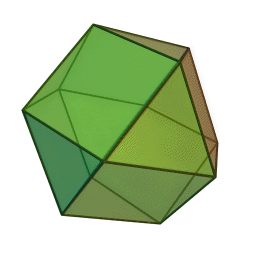
Above is the iconic image of Jyotish, the kuNDali or astrology chart.

It’s beauty is clear and when the planets are placed on it, it is believed to contain the cosmos.

The diamond labelled 1 is what faces the Eastern horizon on the Earth’s surface at the point and time of the chart. Diamond 7 is what faces West, opposite of 1.

The diamond labelled 10 is what is overhead, 4 is what is beneath the feet.

The native and the planet earth’s center is the point in the middle.

The triangles are what are respectively in between the cornerstones 1, 4, 7, and 10. The latter are called kendras.

The first time I saw this I wanted to go home, get paper and scissors, and construct the universe.

I tried, but it isn’t possible to create a 12 sided convex polygon with 4 squares and 8 triangles. The angles and sides just do not add up. There is a platonic solid with twelve sides but it requires a pentagonal face for each of the 12 sides.

What about splitting up the diamonds (squares) each into 2 triangles, thus aspiring to have a 16 sided convex regular polyhedron? Still doesn’t exist, at least not in 3-D.

You can have a regular cuboctagon, but if you look carefully 2 sides would have to be wide open:

How about a slight irregularity? Something called a snub tetrahedron might be the closest to what we are looking for. (Here the yellows are the kendras – 2 triangles per kendra square; while houses 2, 3, 5, 6, and 8,9, 11, 12 stay triangles.)

It’s interesting that the konas (important houses 5, and 9 besides 1) have a physical element with the snub tetrahedron: they would allow a stability of this physical model if set on the “ground” with the yellow 1 triangles pointing up, like it’s on an inner tripod.

Here’s an interesting site on the solid form. If you can get through the first paragraph, go to the animation on the bottom of the page and count to three. At that point the pink triangles show pretty well how to construct the snub.

But I don’t like the word “irregularity” when talking about the universe or of having empty 3-D spaces therein. Plus, “snub” is a funny word.

Also it’s not clear how to take a pair of scissors and cut up the surface of the snub tetrahedron so that it would lie on a 2D surface (such as your screen or your chart) and form something like the kuNDali at the top of this post.

So I did what I could: I looked into the 4th dimension.

Consider the dodecaplex which very importantly is both regular and convex in 4 dimensions, thus satisfying my desire for symmetry and allows for the convex nature of a screen for shining bodies.

I totally recommend installing this software. It is a program that will show you visually a lot more than I can say with words. (Yep, it’s virus free and exceedingly cool.)

[Could the five hyper-sides of each tetrahedron house element have to do with the five Maha Bhutas (five elements)?

Could the icosahedron in 3D that has 20 faces of triangles have to do with the 20gunas of Ayurveda composed of 3 doshas?]

The beautiful complications toward the middle of the dodecaplex could account for the amshas.

Finally, by projection (cross-section or shadow) the snub cuboctahedron or 3-D image we are trying to represent is:

A [snub] cuboctahedron can be obtained by taking an appropriatecross section of a four-dimensional cross-polytope. [i.e., a dodecaplex], Wikipedia

Projection or shining of light seems entirely appropriate to the meaning ofJyotish, especially as compared to cutting something up to form a net.

And corresponding objects exist in even higher dimensions.

Extra dimensions are not a problem in the Vedas – they are talked about often and at length.