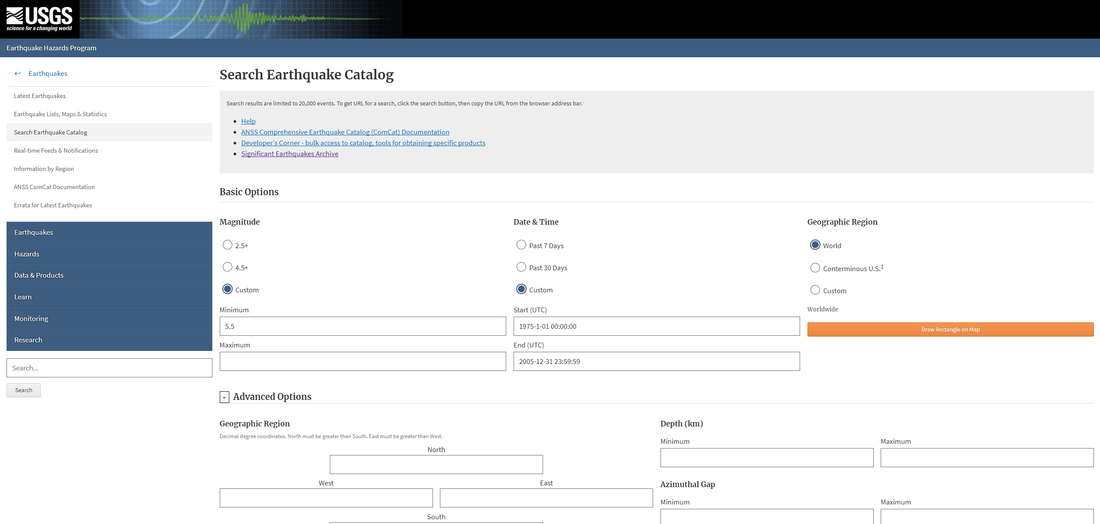
When it comes to modeling real-life phenomena for astrological research, earthquakes are one of the most widely studied.

And why not? After all, the exact time, place, and day are known as well as the strength of the effect (in magnitude).

However, a mapping of earthquake strength to solar system events has proven to be elusive, not to be dramatic, but until now.

Inspired by this Kaggle post, I decided to try my hand at this perhaps age-old problem, and I found that yes, earthquake magnitude correlates with the moon phase at the time of the event. (Moon phase has been looked at quite often but not with the model I will present today.)

First off, I went to https://earthquake.usgs.gov for the earthquake data. (Thanks to Joe Ritrovato for the link.)

​I wanted to look particularly at all earthquakes of any depth between Jan 1, 1975 and Jan 1, 2005. Those years were chosen, because a uniform seismograph was finally used through out the world by the mid-1970's, and hydraulic fracturing with its associated quakes was not yet in widespread practice. The search was further restricted to earthquakes of magnitude greater than 5.5, following this system of what counts as a serious earthquake. (Some lower limit to the magnitudes was necessitated by the search limit on the USGS site.)

Here is what my search looked like (be sure to also choose earthquakes only below the fold):

And here is what you will see if you press enter:

By reading the book Cymatics, many of us thrilled to the idea of vibration made visible in that gem of a book from the late 1960's. 

With a few lines of code I have decided to plot the equations which go to heart of, and could be said to generate, these beautiful forms.

More motivated me than just the chance to look directly at and witness the imagery. I have seen some claims that the Shri Chakra could be seen from these "tonoscopes".